Genaue Erklärung des Aharonov-Bohm-Effektes.
Diese Formel stammt aus dem Aharonov-Bohm-Effekt und beschreibt die Phasenverschiebung (Δϕ) eines quantenmechanischen Teilchens aufgrund eines magnetischen Vektorpotentials A.
Hier die genauen Bedeutungen der Terme:
- Δϕ (Phasenverschiebung)
Dies ist die Änderung der Phase einer quantenmechanischen Wellenfunktion, wenn ein geladenes Teilchen ein Gebiet mit einem elektromagnetischen Potential durchläuft.
Entscheidend: Die Phasenverschiebung tritt auch dann auf, wenn kein direkt messbares Magnetfeld vorhanden ist, der Effekt entsteht allein durch das Vektorpotential A.
- eℏ (Kopplungsfaktor der Ladung mit dem Vektorpotential)
e (Elementarladung)
Die elektrische Ladung eines Elektrons oder Protons (e≈1.602×10−19C).
Gibt an, wie stark das geladene Teilchen mit dem elektromagnetischen Feld wechselwirkt.
ℏ (reduziertes Planck’sches Wirkungsquantum)
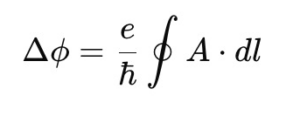
Setzt die Skala für quantenmechanische Effekte.
Normalisiert die Wechselwirkung zwischen dem Teilchen und dem elektromagnetischen Potential.
Zusammen:
Der Term eℏ beschreibt, wie stark ein geladenes Teilchen mit dem elektromagnetischen Vektorpotential A gekoppelt ist.
Dies zeigt, dass die Phasenverschiebung umso größer ist, je stärker die Ladung e oder
das Vektorpotential A ist.
- ∮A⋅dl (Schleifenintegral über das Vektorpotential)
Dies ist das Linienintegral des Vektorpotentials A entlang eines geschlossenen Weges dl.
A (Vektorpotential des Magnetfelds)
Eine fundamentale Größe in der Elektrodynamik.
Beschreibt das elektromagnetische Feld in einer Weise, die über die bloße Existenz eines Magnetfeldes hinausgeht.
In vielen Fällen ist A nicht direkt messbar, aber es beeinflusst trotzdem Quantenphänomene.
∮A⋅d
Wurde ganz klar nachgewiesen
Mehrfach sogar, sowohl mit Elektroneninterferometern als auch in kondensierter Materie (z. B. in supraleitenden Ringen).
Es gibt eindeutige Interferenzverschiebungen, obwohl keine klassische Kraft auf das Elektron wirkt, somit der Beweis des leptonischen Otto-Mediums.